正经博客

在羚珑智能设计工具——程序化设计里，我们需要根据设计师给到的作图规范来绘制对应的图形，通过输入不同的参数输出不同的设计结果，上面背景图就是程序化设计里一个2.5D背景模型生成图片的一些例子。那我们使用的绘图工具就是 skia。

tu1

# 1.Skia

# 1.1 Skia 简单介绍

Skia 是一个开源 2D 图形库，它提供适用于各种硬件和软件平台的通用 API。 它作为 Google Chrome 和 ChromeOS、Android、Flutter 和许多其他产品的图形引擎。Skia 支持多语言调用， C++/C#/Java/Python/Rust/WASM 等。

程序化设计有浏览器端以及服务端的绘制需求，所以我们选择 canvaskit-wasm (opens new window) 这个 Skia 打包出来的供 JS 调用的 WebAssembly NPM 包，在 web 端以及 nodejs 端都能使用，这样就满足了多端的需求。

# 1.2 常用绘图 API

Surface

Surface 是一个对象，用于管理绘制画布命令的内存，通过处理这段内存信息，可以将它转成图片。

下面的代码显示如何加载这个包并进行 API 调用：

import CanvasKitInit from 'canvaskit-wasm'

const loadLib = CanvasKitInit({
  locateFile(file) {
    return 'https://unpkg.com/canvaskit-wasm@0.19.0/bin/' + file
  }
})

loadLib.then(lib => {
  // 创建 500x500 的 surface
  const surface = lib.MakeSurface(500, 500)
  // 获取画布
  const canvas = surface.getCanvas()
})

Canvas

Canvas 是 Skia 绘图上下文，它提供了绘图的接口。

  • canvas.drawRect()：绘制一个矩形
  • canvas.drawCircle()：绘制一个圆
  • canvas.drawLine()：绘制一条直线
  • canvas.drawPath()：绘制一条路径
  • canvas.drawArc()：绘制一条圆弧
  • canvas.drawText()：绘制文字
  • ...

Path

Path 绘制路径。

  • path.moveTo(x, y)：从(x,y)开始绘制一个路径
  • path.lineTo()：将直线添加到路径
  • path.arcTo()：将弧线添加到路径
  • path.cubicTo()：添加贝塞尔曲线
  • path.quadTo()：添加二次贝齐尔曲线
  • path.close()：闭合路径
  • path.addRect()：添加一个矩形到路径
  • path.addCircle()：添加圆
  • path.addOval()：添加椭圆
  • path.addRoundedRect()：添加圆角矩形
  • path.addArc()：添加圆弧
  • path.addPath()：添加另一个路径
  • ...

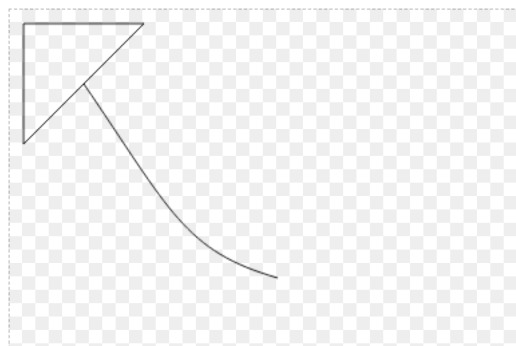
Path 绘制例1：

// 绘制三角形
const path = new CanvasKit.Path()
path.moveTo(10, 10)
path.lineTo(100, 10)
path.lineTo(10, 100)
path.close()

// 绘制贝塞尔曲线
const arcPath = new CanvasKit.Path()
arcPath.moveTo(55, 55)
arcPath.cubicTo(120, 150, 130, 180, 200, 200)

// 添加曲线路径
path.addPath(arcPath)

canvas.drawPath(path, paint) // paint 画笔，见下文

绘制结果：

exp1

Paint

Paint 画笔，用于存储当前绘制图形的样式信息。

  • paint.setColor()：设置画笔颜色
  • paint.setAlphaf()：设置透明度
  • paint.setAntiAlias()：抗锯齿
  • paint.setBlendMode()：设置混合模式
  • paint.setStyle()：设置画笔样式
  • paint.setStrokeWidth()：设置描边宽度
  • paint.setColorFilter()：设置颜色筛选器
  • paint.setImageFilter()：设置图像筛选器
  • paint.setMaskFilter()：设置掩码筛选器
  • paint.setShader()：设置着色器
  • ...

例1 中需要加上 Paint 进行样式绘制：

const { Path, parseColorString } = CanvasKit

const paint = new Paint()
paint.setStyle(PaintStyle.Stroke)
paint.setColor(parseColorString('#000000'))

canvas.drawPath(path, paint)

Shader

Shader 着色器，用于绘制渐变、噪声、平铺等效果。

  • shader.MakeColor()：设置着色器颜色
  • shader.MakeLinearGradient()：线性渐变
  • shader.MakeRadialGradient()：径向渐变
  • shader.MakeSweepGradient()：扫描渐变
  • shader.MakeTwoPointConicalGradient()：两点圆锥渐变
  • shader.MakeFractalNoise()：柏林噪声
  • shader.MakeTurbulence()：平铺柏林噪声
  • shader.MakeBlend()：组合多个着色器效果

Shader 绘制例2：

const { Shader, parseColorString, TileMode } = CanvasKit

const shader = Shader.MakeLinearGradient(
  [0, 0], // 渐变开始点
  [50, 50], // 渐变结束点
  [
    parseColorString('#ff0000'),
    parseColorString('#ffff00'),
    parseColorString('#0000ff')
  ], // 渐变颜色
  [0, 0.5, 1], // 颜色范围比例
  TileMode.Clamp, // 范围外颜色样式模式
)

paint.setShader(shader)

绘制结果：

jianbian

Blendmode

Blendmode 混合模式，用于确定当两个图形对象互相重叠时需要如何绘制。主要分为三大类：

Porter-Duff 分离 不可分离
Clear Modulate Hue
Src Overlay Saturation
Dst Darken Color
SrcOver Lighten Luminosity
DstOver ColorDodge -
SrcIn ColorBurn -
DstIn HardLight -
SrcOut SoftLight -
DstOut Difference -
SrcATop Exclusion -
DstATop Multiply -
Xor - -
Plus - -

  1. Porter-Duff 模式：通常用于执行裁剪操作

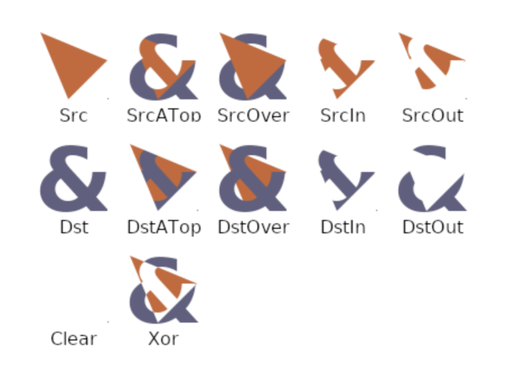
    Porter-Duff

  2. 可分离混合模式：可以混合颜色，通常用于照亮或变暗图像。

    fenli

  3. 不可分离混合模式：可以混合颜色，通常通过对色调、饱和度和亮度颜色级别进行操作。

    bukefenli

Matrix

Matrix 矩阵工具，用于图形变换、数学计算等，主要有三个：

  1. ColorMatrix: 用于计算颜色
  2. Matrix: 3x3矩阵计算，常用于二维图形变换
  3. M44: 4x4矩阵计算，三维图形变换

矩阵是图形变换不可或缺的计算工具，接下来详细阐述一下关于二维图形变换的工具——Matrix。

# 2. 图形变换

所有的图形变换本质上是点的坐标变换，即：

(x, y) => (x', y')

要实现点的坐标变换，需要借助一个中间矩阵与坐标点相乘之后得到变换结果：

(x, y) × 中间矩阵 = (x', y')

在 Skia 中需要借助一个 3x3 的矩阵进行坐标变换（原因见下文）：

                │ ScaleX  SkewY   Persp0 │
| x  y  1 |  ×  │ SkewX   ScaleY  Persp1 │ = | x'  y'  z' |
                │ TransX  TransY  Persp2 │

这里可以理解为在三维的某个面上进行图形变换，为了方便计算，我们将 z 值设为 1，相当于在 z 值为 1 的平面上进行变换：

z' = 1
xFinal = x' / z' = x'
yFinal = y' / z' = y'

最后就得到了最终变换的结果：

(x, y) => (xFinal, yFinal)

Skia 中也提供了一个方便的方法实现坐标变换：

Matrix.mapPoints(mat, [x, y]) // 得到经 mat 矩阵变换之后的 x/y 坐标

Skia 中的坐标系与经典直角坐标系（笛卡尔坐标系）有所区别，它的 y 轴正方向是向下的，所以变换矩阵也有一些区别。

接下来详细介绍一下常见的图形变换。

# 2.1 平移变换

平移变换在水平方向和垂直方向移动图形对象，如下图宽高为 1 的矩形（单位矩形）由 (0,0) 点向 x 轴移动到 X，向 y 轴移动到 Y：

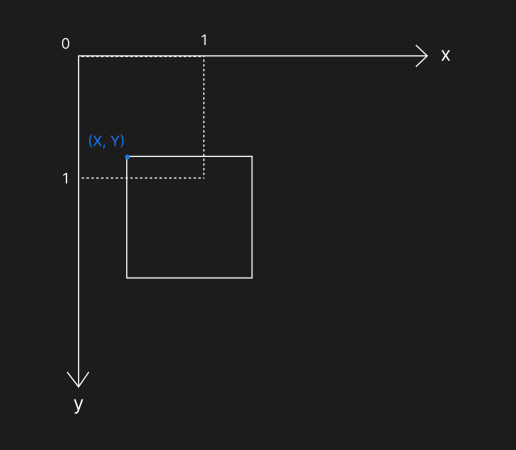
pingyi

平移变换的中间矩阵：

                │ 1  0  0 │
| x  y  1 |  ×  │ 0  1  0 │ = | x'  y'  1 |
                │ X  Y  1 │

这里可以解释一下为何需要使用 3x3 矩阵去做变换，是因为二维矩阵无法表达 平移 这种最基础的图形变换，2x2 矩阵表示两个维度中的线性变换，线性变换无法改变 (0,0)，所以需要借助升维来解决。见参考资料 (opens new window)。

在 Skia 中可以使用 Matrix.translated() 方法来方便做平移变换：

Matrix.translated(X, Y)

# 2.2 缩放变换

缩放变换会更改图形对象的大小，如下图矩形在 x 方向上缩放了 W 倍，在 y 方向上缩放了 H 倍：

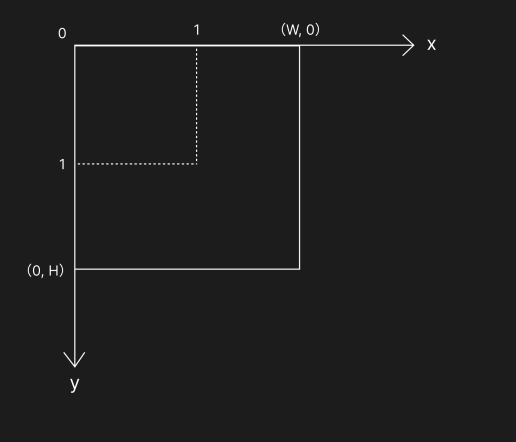
bukefenli

缩放变换的中间矩阵：

                │ W  0  0 │
| x  y  1 |  ×  │ 0  H  0 │ = | x'  y'  1 |
                │ 0  0  1 │

在 Skia 中可以使用 Matrix.scaled() 方法来方便做缩放变换：

Matrix.scaled(W, H)

# 2.3 旋转变换

旋转变换使图形围绕某个点进行旋转，如下图矩形围绕着 (0,0) 旋转了 θ 度：

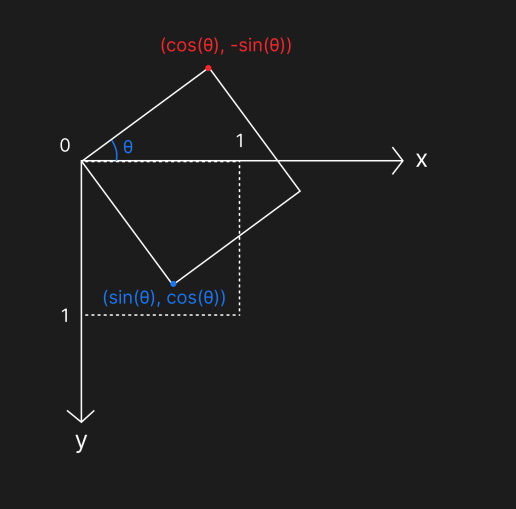
bukefenli

旋转变换的中间矩阵：

                │  cos(θ)  sin(θ)  0 │
| x  y  1 |  ×  │ -sin(θ)  cos(θ)  0 │ = | x'  y'  1 |
                │    0       0     1 │

在 Skia 中可以使用 Matrix.rotated() 方法来方便做旋转变换：

Matrix.rotated(toRadians(θ), 0, 0) // 需要将角度转换为弧度

# 2.4 倾斜变换

倾斜变换可以使图形在水平或垂直方向上倾斜。

如下图在垂直方向上倾斜了 α 度：

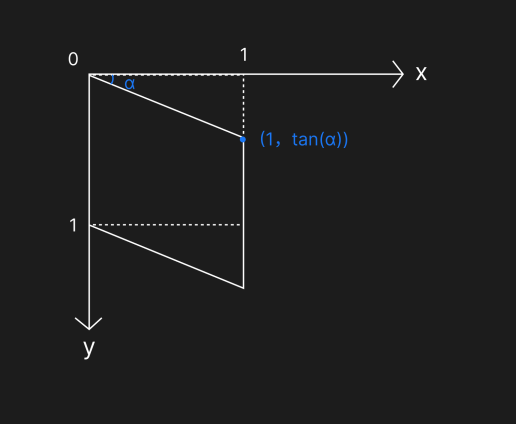
bukefenli

下图在水平方向上倾斜了 θ 度：

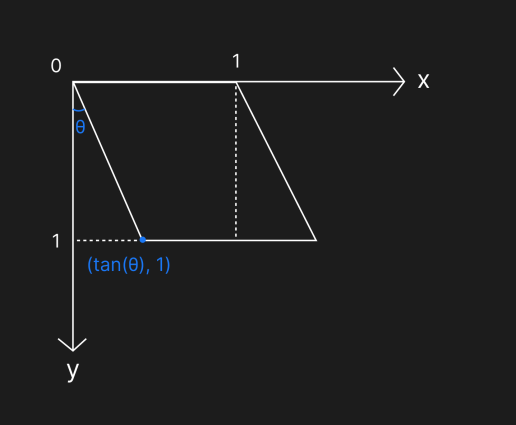
bukefenli

倾斜变换的中间矩阵：

                │    1     tan(α)  0 │
| x  y  1 |  ×  │  tan(θ)    1     0 │ = | x'  y'  1 |
                │    0       0     1 │

在 Skia 中可以使用 Matrix.skewed() 方法来方便做倾斜变换：

Matrix.skewed(tan(α), tan(θ), 0, 0)

# 2.5 透视变换

透视变换可以实现图形的透视效果，它可以使矩形变换成任意凸四边形，下图将底边在水平方向分别扩展了 X1、X2 的距离：

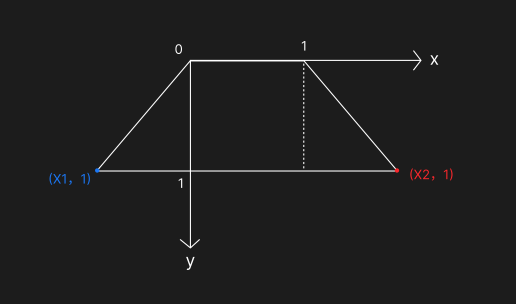
bukefenli

由此，我们可以知道变换前以及变换后每个顶点的坐标，通过这些坐标值，可以计算透视中间矩阵。

首先，通过 Skia 的中间矩阵变换计算可以得到以下公式：

x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2

xFinal = x' / z'
yFinal = y' / z'
z' = 1

于是可以得到 xFinal, yFinal:

xFinal = (ScaleX·x + SkewX·y + TransX) / (Persp0·x + Persp1·y + Persp2)
yFinal = (SkewY·x + ScaleY·y + TransY) / (Persp0·x + Persp1·y + Persp2)

将变换前的 (0, 0)、(w, 0)、(0, h)、(w, h) 以及变换后的 (x1, y1)、(x2, y2)、(x3, y3)、(x4, y4) 代入公式：

x1 = (ScaleX·0 + SkewX·0 + TransX) / (Persp0·0 + Persp1·0 + Persp2)
y1 = (SkewY·0 + ScaleY·0 + TransY) / (Persp0·0 + Persp1·0 + Persp2)

x2 = (ScaleX·w + SkewX·0 + TransX) / (Persp0·w + Persp1·0 + Persp2)
y2 = (SkewY·w + ScaleY·0 + TransY) / (Persp0·w + Persp1·0 + Persp2)

x3 = (ScaleX·w + SkewX·h + TransX) / (Persp0·w + Persp1·h + Persp2)
y3 = (SkewY·w + ScaleY·h + TransY) / (Persp0·w + Persp1·h + Persp2)

x4 = (ScaleX·0 + SkewX·h + TransX) / (Persp0·0 + Persp1·h + Persp2)
y4 = (SkewY·0 + ScaleY·h + TransY) / (Persp0·0 + Persp1·h + Persp2)

简化之后：

x1·Persp2 - TransX = 0
y1·Persp2 - TransY = 0

Persp0·w·x2 + Persp2·x2 - ScaleX·w - TransX = 0
Persp0·w·y2 + Persp2·y2 - SkewY·w - TransY = 0

Persp0·w·x3 + Persp1·h·x3 + Persp2·x3 - ScaleX·w - SkewX·h - TransX = 0
Persp0·w·y3 + Persp1·h·y3 + Persp2·y3 - SkewY·w - ScaleY·h - TransY = 0

Persp1·h·x4 + Persp2·x4 - SkewX·h - TransX = 0
Persp1·h·y4 + Persp2·y4 - ScaleY·h - TransY = 0

最后，将具体的坐标值代入，就能将最终值求解出。

以下是最终参考计算方法：

export type Point = { x: number; y: number }

export function createPerspectiveMatrixFromPoints(
  topLeft: Point,
  topRight: Point,
  botRight: Point,
  botLeft: Point,
  w: number,
  h: number,
) {
  const { x: x1, y: y1 } = topLeft
  const { x: x2, y: y2 } = topRight
  const { x: x3, y: y3 } = botRight
  const { x: x4, y: y4 } = botLeft

  const scaleX =
    (y1 * x2 * x4 -
      x1 * y2 * x4 +
      x1 * y3 * x4 -
      x2 * y3 * x4 -
      y1 * x2 * x3 +
      x1 * y2 * x3 -
      x1 * y4 * x3 +
      x2 * y4 * x3) /
    (x2 * y3 * w + y2 * x4 * w - y3 * x4 * w - x2 * y4 * w - y2 * w * x3 + y4 * w * x3)
  const skewX =
    (-x1 * x2 * y3 -
      y1 * x2 * x4 +
      x2 * y3 * x4 +
      x1 * x2 * y4 +
      x1 * y2 * x3 +
      y1 * x4 * x3 -
      y2 * x4 * x3 -
      x1 * y4 * x3) /
    (x2 * y3 * h + y2 * x4 * h - y3 * x4 * h - x2 * y4 * h - y2 * h * x3 + y4 * h * x3)
  const transX = x1
  const skewY =
    (-y1 * x2 * y3 +
      x1 * y2 * y3 +
      y1 * y3 * x4 -
      y2 * y3 * x4 +
      y1 * x2 * y4 -
      x1 * y2 * y4 -
      y1 * y4 * x3 +
      y2 * y4 * x3) /
    (x2 * y3 * w + y2 * x4 * w - y3 * x4 * w - x2 * y4 * w - y2 * w * x3 + y4 * w * x3)
  const scaleY =
    (-y1 * x2 * y3 -
      y1 * y2 * x4 +
      y1 * y3 * x4 +
      x1 * y2 * y4 -
      x1 * y3 * y4 +
      x2 * y3 * y4 +
      y1 * y2 * x3 -
      y2 * y4 * x3) /
    (x2 * y3 * h + y2 * x4 * h - y3 * x4 * h - x2 * y4 * h - y2 * h * x3 + y4 * h * x3)
  const transY = y1
  const persp0 =
    (x1 * y3 - x2 * y3 + y1 * x4 - y2 * x4 - x1 * y4 + x2 * y4 - y1 * x3 + y2 * x3) /
    (x2 * y3 * w + y2 * x4 * w - y3 * x4 * w - x2 * y4 * w - y2 * w * x3 + y4 * w * x3)
  const persp1 =
    (-y1 * x2 + x1 * y2 - x1 * y3 - y2 * x4 + y3 * x4 + x2 * y4 + y1 * x3 - y4 * x3) /
    (x2 * y3 * h + y2 * x4 * h - y3 * x4 * h - x2 * y4 * h - y2 * h * x3 + y4 * h * x3)
  const persp2 = 1

  return [scaleX, skewX, transX, skewY, scaleY, transY, persp0, persp1, persp2]
}

# 3 绘制举例

拿文章开头 2.5D 模型的例子，来绘制一个这样的图形：

bukefenli

# 3.1 图层分析

这个图形主要由上下两部分组成。上部分由一个渐变背景层以及一个方格覆盖层组成，需要进行背景颜色渐变以及方格绘制；下部分由一个渐变背景层以及一个棋盘格覆盖层组成，同样需要背景颜色渐变以及方格绘制，同时图形有透视效果，需要进行透视变换。

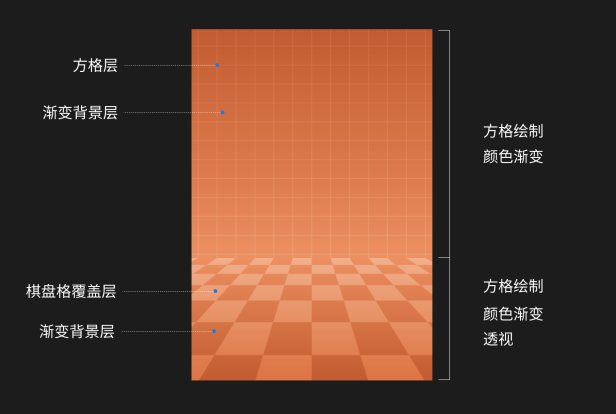
bukefenli

由此，可以将该图形拆解成上下两个部分，因为同样由方格层以及背景层组成，其实可以将之绘制成一个图形，通过输入不同的参数进行变化（透视、方格填色）。

# 3.2 图形绘制

背景层

  • 给整个图形画一个方框，加上渐变着色器即完成背景绘制。
const backgroundPaint = new Paint()
backgroundPaint.setStyle(PaintStyle.Fill)

const points = {
  begin: [0, height],
  end: [0, 0],
}

const colors = [parseColorString(beginColor), parseColorString(endColor)]
const shader = Shader.MakeLinearGradient(points.begin, points.end, colors, [0, 1], TileMode.Clamp) // 渐变

backgroundPaint.setShader(shader)

// 绘制矩形
canvas.drawRect(Rect.makeXYWH(0, 0, width, height).toArray(), backgroundPaint)

绘制结果：

bukefenli

方格层

  • 根据画布宽高和间距计算出 x 方向和 y 方向上绘制的方格个数 + 1，然后根据奇偶数排列绘制矩形，并使用平移矩阵将整体居中。
  • 针对方格层图形进行渐变颜色填充或线条颜色填充绘制。
const rectsPath = new Path()
for (let i = 0; i < lineNum + 1; i++) { // 循环遍历绘制方格
  for (let j = 0; j < yLineNum + 1; j++) {
    if (i % 2 === 0 && j % 2 === 0) {
      const rect = Rect.makeXYWH(rectSize * i, rectSize * j, rectSize, rectSize)
      rectsPath.addRect(rect.toArray())
    }

    if (i % 2 === 1 && j % 2 === 1) {
      const rect = Rect.makeXYWH(rectSize * i, rectSize * j, rectSize, rectSize)
      rectsPath.addRect(rect.toArray())
    }
  }
}

const overlayShader =  Shader.MakeLinearGradient( // 方格层渐变
  points.begin,
  points.end,
  overlayColors,
  [0, 1],
  TileMode.Clamp,
)

const rectsPaint = new Paint()
rectsPaint.setAntiAlias(true)
rectsPaint.setStyle(PaintStyle.Stroke)
rectsPaint.setShader(overlayShader)

canvas.drawPath(rectsPath, rectsPaint)

绘制结果：

bukefenli

棋盘方格

  • 棋盘方格只需要将方格层绘制样式设置为填充即可。
rectsPaint.setStyle(PaintStyle.Fill)

canvas.drawPath(rectsPath, rectsPaint)

绘制结果：

bukefenli

透视方格

  • 将方格层加上透视变换即可实现透视效果。
// 透视矩阵
const m = getPerspectiveMatrix(width, height)
// 矩阵变换
rectsPath.transform(m)

canvas.drawPath(rectsPath, rectsPaint)

绘制结果：

bukefenli

图形组合

  • 将方格层图形与透视方格图形组合。
<>
  <PerpectiveRect
    width={512}
    height={450}
    beginColor={c0}
    endColor={c3}
    isGradient
  />
  <PerpectiveRect
    width={512}
    height={300}
    beginColor={c0}
    endColor={c3}
    isGradient      // 是否渐变
    isPerspective   // 是否透视
    isXRect         // 是否棋盘格
  />
</>

绘制结果：

bukefenli

# 参考资料

skia.org (opens new window)

https://learn.microsoft.com/en-us/xamarin/xamarin-forms/user-interface/graphics/skiasharp/ (opens new window)

https://stackoverflow.com/questions/48416118/perspective-transform-in-skia (opens new window)

← 基于 MF 的组件化共享工作流 - Qcon 广州演讲整理 →